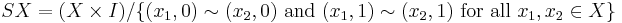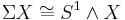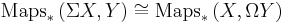Suspension (topology)

In topology, the suspension SX of a topological space X is the quotient space:

SX = (X \times I)/\{(x_1,0)\sim(x_2,0)\mbox{ and }(x_1,1)\sim(x_2,1) \mbox{ for all } x_1,x_2 \in X\}

of the product of X with the unit interval I = [0, 1]. Intuitively, we make X into a cylinder and collapse both ends to two points. One views X as "suspended" between the end points. One can also view the suspension as two cones on X glued together at their base (or as a quotient of a single cone).

Given a continuous map 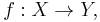f:X\rightarrow Y, there is a map 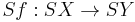Sf:SX\rightarrow SY defined by Sf([x,t]):=[f(x),t]. This makes S into a functor from the category of topological spaces into itself. In rough terms S increases the dimension of a space by one: it takes an n-sphere to an (n + 1)-sphere for n ≥ 0.

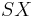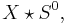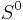Note that SX is homeomorphic to the join X\star S^0, where S^0 is a discrete space with two points.

The space 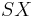SX is sometimes called the unreduced, unbased, or free suspension of X, to distinguish it from the reduced suspension described below.

The suspension can be used to construct a homomorphism of homotopy groups, to which the Freudenthal suspension theorem applies. In homotopy theory, the phenomena which are preserved under suspension, in a suitable sense, make up stable homotopy theory.

Reduced suspension

If X is a pointed space (with basepoint x0), there is a variation of the suspension which is sometimes more useful. The reduced suspension or based suspension ΣX of X is the quotient space:

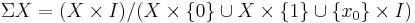\Sigma X = (X\times I)/(X\times\{0\}\cup X\times\{1\}\cup \{x_0\}\times I).

This is the equivalent to taking SX and collapsing the line (x0 × I) joining the two ends to a single point. The basepoint of ΣX is the equivalence class of (x0, 0).

One can show that the reduced suspension of X is homeomorphic to the smash product of X with the unit circle S1.

\Sigma X \cong S^1 \wedge X

For well-behaved spaces, such as CW complexes, the reduced suspension of X is homotopy equivalent to the ordinary suspension.

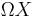Σ gives rise to a functor from the category of pointed spaces to itself. An important property of this functor is that it is a left adjoint to the functor \Omega taking a (based) space X to its loop space \Omega X. In other words,

\operatorname{Maps}_*\left(\Sigma X,Y\right)\cong \operatorname{Maps}_*\left(X,\Omega Y\right)

naturally, where 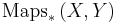\operatorname{Maps}_*\left(X,Y\right) stands for continuous maps which preserve basepoints. This is not the case for unreduced suspension and free loop space.

See also

References